About the program
The purpose of this simulator is to experiment with cellular automata (analogs of Game of Life), living on the Minkowski plane: an analog of the Euclidean plane governed by the pseudo-euclidean distance (note the minus sign):
$$d((x_1,y_1),(x_2,y_2)) = (x_1-x_2)^2-(y_1-y_2)^2.$$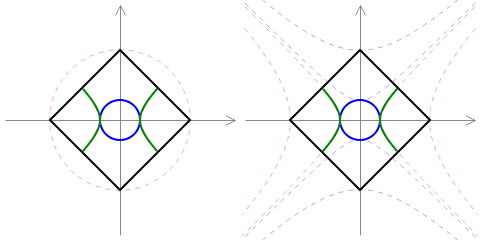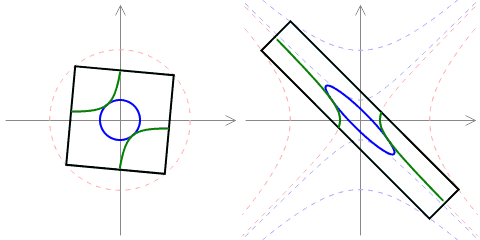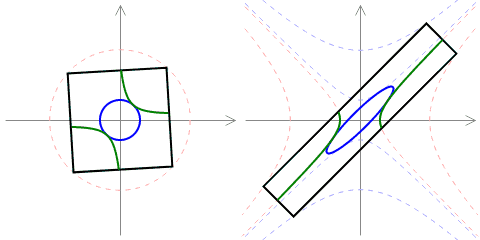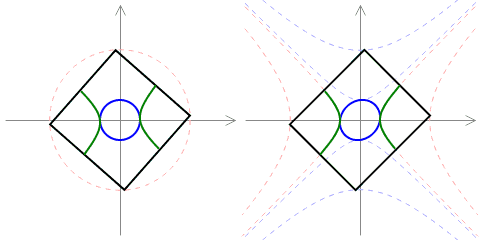
World
Lattice matrix
Cellular automata in this simulator live on a lattice of regularly spaced points with a certain rotational symmetry. In the Euclidean plane, there are two such lattices: square lattice having 4-fold rotational symmetry and hexagonal lattice having 6-fold symmetry. However, in the Minkowski plane there is infinite number of such lattices.
It might be not obvious, but such lattices (both Euclidean and Minkowskian) are identified by the integer matrices of determinant 1, also known as the elements of the special linear group \(SL(2,\mathbb{Z})\).
$$M=\left(\begin{matrix}a && b\\c && d\end{matrix}\right), |M|=ad-bc=1,$$ $$a,b,c,d \in \mathbb{Z}.$$This, however, is not a one-to-one relation, since different matrices could define the same lattice. Particularly, congruent matrices generate the same lattice. The trace of the matrix (the sum of its diagonal elements \(a+c\)) determines lattice type: if \(|tr(M)|<2\), then the lattice is Euclidean, and if \(|tr(M)|>2\) then it is Minkowskian. The case when \(tr(M)=\pm 2\) is degenerate and not supported by the simulator.
In the simulator, Lattice matrix field defines the lattice. It must contain four integers separated by spaces, in row-major order: "a b c d".
Some matrices and their lattices:
| Matrix | Lattice |
|---|---|
| \(\left(\begin{matrix}0 && -1\\1 && 0\end{matrix}\right)\) | Euclidean square lattice |
| \(\left(\begin{matrix}1 && 1\\-1 && 0\end{matrix}\right)\) | Euclidean hexagonal lattice |
| \(\left(\begin{matrix}2 && 1\\1 && 1\end{matrix}\right)\) | The simplest Minkowskian lattice |
Neighbors
In cellular automata, cell state is affected by the states of its neighbors. In this simulator, all cells at the certain distance are considered neighbors. It is also possible to specify several distances. Instead of specifying the distance directly (which proved to be inconvenient), a list of sample neighbor coordinates is given. The format of the list is "x1 y1;x2 y2;..."
Cell coordinates are not obvious, to see them enable Draw tool and hover the mouse above the grid. Text in the bottom left corner of the view displays cell coordinates. Alternatively, use Cue tool and select some cell. Cell coordinates are displayed at the same place
Interface
Some tools on the top toolbar are grouped in pairs. When using mouse, left mouse button activates the selected tool, and right mouse button activates its pair.
Editing cells
Enable Draw tool and use mouse do toggle cells. When using custom rules with more than two states, additional buttons allowing to select state are shown. Draw tool hotkey is D.
Running the automaton
To run the simulation for one step, use the Step button. Its hotkey is N. If the calculation takes long time, a button allowing to cancel the simulation appears.
To undo the last simulation step, press Z.
To run the simulation continuously, click Go button.
Random configuration
To generate random configuration of cells, use controls in the "Randomize" section of the left panel. Enter the size of the random block, and the density of "alive" cells, then click Random fill. The hotkey is A.
Using cue mark
Use Cue mark tool to select a cell and see its neighbors. Neighbor cells are shown with empty circles; curves of equal distance are shown by dashed lines. Cue cool hotkey is U. Alternatively, use Draw tool and right mouse button to put cue mark. To remove cue mark, put it on the same place, or click Hide button on the top toolbar.
Copying and pasting
To copy a configuration of cells, activate Copy tool on the top toolbar, and drag mouse over it. Selected configuration of cells is put into the "buffer" text area on the left control panel. Hotkey is C.
To paste a copied configuration, Paste tool and click where to paste it. Hotkey is P.
Navigation: pan, zoom, rotate
Use Pan tool to drag the view using the mouse. Alternatively, hold Ctrl key and drag mouse - this method works when any other tool is active
Use Rotate tool or drag mouse left and right holding Shift to rotate the view around the center. When Euclidean lattice matrix is used, this tool does a familiar Euclidean rotation. When the matrix is Minkowskian, it does pseudo-rotation (squeeze mapping).
To zoom the view in and out, either use mouse wheel or buttons Zoom In/Out on the left control panel.
"Navigator" section of the left control panel shows current position and rotation of the view. Rotation angle is in degrees; when Minkowskian lattice is active, rotation angle could be arbitrarily high or low: unlike Euclidean rotation, pseudo-rotation does not loops after 360°.
Adjusting the display
Several buttons on the left panel control the appearance of the view:
- C - show lines, connecting neighbor cells. In Minkowskian lattices, neighbors are not obvious.
- E - show empty cells, i. e. the cells whose state is 0.
- X - show cross in the view center.
- N - show numbers instead of colored dots.
The slider above them controls the size of the colored circle of the cell image.
Exporting data
There are two ways to export data from the simulator. The first one is to use Copy tool and then copy the text from the "Buffer" text area. This text can be stored, then pasted back to the buffer.
The other way is to export current simulator state to the URL using the Save to url... button. It generates an URL that encodes current world state, rule and view position.
Custom rules
Custom rules allow to run custom automata with any number of states and user-defined transition rules. They need not be totalistic. To enable custom rule, click Custom rule... button and edit the code. Click Basic sample / Complex sample buttons to load sample code.
Custom rule is defined by a JavaScript object having following fields:
next: required, its type isfunction(state, sumNeighbors) -> newState. Calculates new state of a cell from its current state and (generalized) sum of the neighbors.states: optional integer, number of states in the automaton. Default value is 2.foldInitial: optional, any type. Initial values for calculating generalized sum of neighbors. Default value is 0.fold: optional,function(sum, state) -> updatedSum. Function to calculate generalized sum of the neighbors. Adds one neighbor state to the sum. Default is plain summation:function(sum,s){return sum+s;}.
Note that the order of neighbor summation is not defined. Also, only cells with nonzero state are summed.
Shortcuts overview
| Editing | |
| N | Next step |
| Z | Undo last step |
| G | Run/stop simulation |
| A | Random fill |
| E | Clear the world |
| Mouse tools | |
| D | Enable drawing mode |
| U | Enable cue mark mode |
| M | Enable panning mode |
| R | Enable rotation mode |
| C | Enable select and copy mode |
| P | Enable paste mode |
| Viewing and navigation | |
| Q | Hide cue mark if shown |
| H | Havigate to origin |
| [ | Zoom in |
| ] | Zoom out |
References
- Mind-blowing "Dichronauts" novel by Greg Egan that inspired this piece of software.
- Sources at the Github.